そろばんの掛け算のコツとは？ ～早く解くためのポイント～

そろばんをやっていると、「どうすればもっとうまくなれるんだろう」「どうやったら友達よりうまくなるんだろう」と考えたことがあると思います。

掛け算がうまくなりたいという同じ一つの悩みでも、内容は人それぞれです。

もっと正答率を上げたい。
もっと早く解けるようになりたい。

同じ早く解けるようになりたいという悩みでも、学習している級によってその答えは変わります。

例えば掛け算を習い始めたての人であれば、九九を早く覚える必要があります。

一方で段位の人であれば、解き方や解く順番を変えることでその悩みを解消することが出来るかもしれません。

そのため、これこそがそろばんの掛け算のコツだ！

と１つのことを断言することはとても難しいですが、今回はなるべくレベルや悩みを分けて、それぞれに対する簡単なアドバイスを紹介します。

後半になるにつれて、上級者向けのものになります。

正答率を上げたい

珠運び

そろばんの掛け算は九九と足し算から構成されています。

そのため、どこのそろばん教室も足し算と引き算(見取り算)が一通り出来るようになったら掛け算を教えると思います。

そのときに足し算の珠運びが苦手だと、やはり掛け算の正答率は下がります。

５＋８など苦手な計算パターンや、珠運びが怪しいときはありませんか？

掛け算の習い始めは掛け算というよりも、足し算がまだ怪しい場合があるので、丁寧に計算しましょう！

位取り

小数の問題でなくとも、位取りは大切です。

６級や５級の人はまずはしっかりと計算後に位取りを確認する習慣を身につけましょう！

位取りをしないがゆえに10点、20点と失う可能性があります。

子供の場合はわかっているつもりでも、知識があいまいなケースがあります。

しっかりと理解させて、一人でも間違えないようにしなければいけません。

早く解けるようになりたい

九九

掛け算を習い始めの場合、九九に時間がかかっていると当然ながら掛け算は早く解けません。

初めは順番通りで覚えると思いますが、そのあとは８×３は？６×７は？などと九九をぶつ切りにして瞬時に答えを出せるようにならなければいけません。

こちらも６級や５級のレベルだと、かなり個人差が出ます。

掛け算を解くスピードに差が出ます。

下記のような百マス計算の九九バージョン(九九マス計算)などを活用すると、早く身につけることが出来ます。

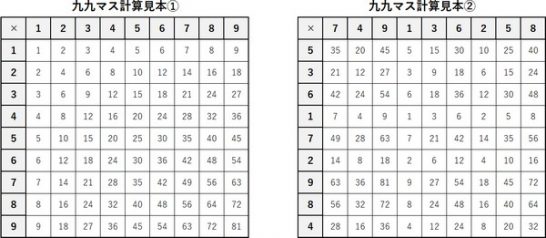
問題を覚える

このあたりから徐々に上級者向けになります。

級で分けるなら４級以上といったあたりでしょうか。

もちろん九九がすらすらと出てきて、足し算の珠運びもスムーズに行えることが前提になります。

いよいよ計算スピードを上げるコツとも言える、テクニック面についてです。

それが問題を覚えるになります。

正確には「問題を見る回数を減らしましょう」となります。

これは例えば648×2,951という問題であれば、片落としでは８×２、８×９、８×５、８×１という順番で計算します。

このときに毎回掛ける数2,951を見ながら(確認しながら)計算するのではなく、2,951を(一瞬で)覚えて、８×２…と計算していくのです。

もちろんこの問題は４級程度のレベルなので、４級の人がいきなり2,951の４桁を頭の中に入れて計算することは難しいと思います。

それでも29と51に分けて、８×２、８×９、目で問題を確認。

その後、８×５、８×１といったように２回で計算したいところです。

掛ける数が３桁であれば、確認するのは１回まで。

４～６桁なら２回までといったところが一つの目安でしょうか。

もちろんこれが１級や段位の人になれば、６桁ぐらいまでは一息で計算したいところです。

これが出来るようになると問題を解くスピードが上がります。

両落としの方は掛けられる数になります。

今回は648なので、２×６、２×４、２×８まで一息で計算したいところです。

解く順番

さらに上級者の人は問題を解く順番を変えるだけでも、解ける問題数を増やすことが出来ます。

級の目安としては２級以上といったところか。(本音は段位以上)

一つは後半の整数で答えを記入する問題を先に解く方が、１番から順に解くよりも解ける問題数は増えるでしょう。

これは多くのそろばん学習者が実践していると思います。

続いて以下の２問で考えます。

こちらは日珠連の１級の見本問題です。

答えは小数第３位までの数にします。

この２つの問題であれば、圧倒的に18番の問題の方が早く解くことが出来ます。

まずは目で見て分かるように、解答に必要な文字数が少なくて済むからです。

掛け算の場合、整数の問題は答えの文字数が多くなります。

それに対して１未満の小数×１未満の小数の場合、四捨五入をするので答えが「0.012」と４文字で済みます。

この答えを記入する時間も掛け算の場合は大きな差になります。

また、答えの書き直しも馬鹿に出来ない時間ロスの原因になります。

さらに１未満の小数×１未満の小数の問題は問題画像のように、式を省略しても答えが合うのです。

どれくらい省略していいのかは問題によりますが、１級の問題であれば左右１桁ずつは概ね大丈夫です。

今回は２桁ずつ省略しても正解なのですが、通常はかなりリスクが高まります。

このへんはいろいろな問題で数パターン試してみると、さじ加減がわかるようになります。

こういった問題の性質を知っていることで、例えばこのような問題を最初に解くだけで、いつもよりも１問多く解けるようになるかもしれません。

どういった問題だと早く解けるのかを意識して練習するといいでしょう。

いろいろと試してみることをおすすめします。