そろばんの割り算の位取り解説

ここではそろばんの割り算の位取りについて解説をします。

掛け算(片落とし)の位取り同様にとても簡単な内容になっています。

というよりも結論から書いてしまうと、掛け算と左右が逆になるだけです。

なので、掛け算を片落としで解いている方は確認程度に軽く読み進めて下さい！

動画では問題の計算経過を見ることが出来ます。

今回の位取りに注意しなければいけない問題を集めた練習用のプリントを用意しましたので、学習後はご活用下さい！

⇒⇒割り算の位取り練習用プリントをダウンロード

位取りとは？

ではここから解説に移りますが、改めて位取りとは何のことかをおさらいします。

位取りとは答えの一の位の桁を特定する方法です。

そろばんで掛け算や割り算を計算すると、答えの一の位が元の定位点と別の桁になります。

その正しい位置を特定するのに必要な知識なります。

問題の答えが3,400なのか、それとも34,000なのかをしっかりと特定するためにそろばんには位取りが必須になります。

そして位取りは大きく２つに分ける事が出来ます。

それが整数と小数です。

割る数が整数のときの位取り

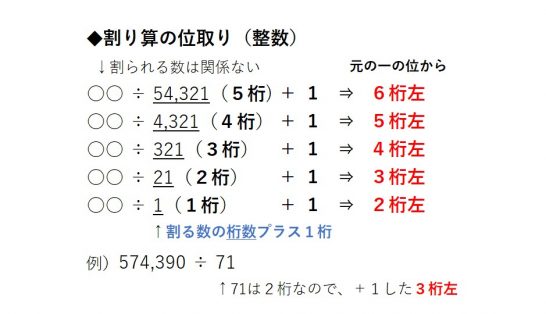
まずは割る数が整数のときの位取りを確認します。

ちなみに位取りを考える際は、割られる数は関係なく、式の右側にある割る数のみを使います。

そしてこの割る数の桁数に＋１をします。

そして元の一の位から＋１をした桁数左が答えの一の位になります。

割り算は元の数の左側に答えを入れるので、左になります。

では例題の574,390÷71を使って確認してみましょう！

今回は計算過程は省略します。

こちらが問題を解く前の574,390をそろばんに入れた状態です。

当然ですが、元の一の位は０がある桁になります。

こちらは574,390÷71を計算したあとの状態です。

計算が終わったら位取りを行います。

今回は割る数が71と２桁の数です。

よって＋１をした、元の一の位から３桁左の桁が答えの一の位になります。

よってこの問題の答えを8,090と特定することが出来ました。

この位取りの知識が曖昧なままだと、答えを809や80,900としてしまいます。

割る数が小数のときの位取り

続いて割る数が小数のときを確認します。

小数のときはその数が１以上なのか、又は１未満なのかで分かれます。

まずは１以上のケースを紹介します。

割る数が１以上の小数の場合

１以上の場合は、先ほどの整数の時とほとんど変わりません。

というのも小数点以下は無視して構わないからです。

例題の20.992÷32.8であれば、割る数は32.8ですが、計算後の位取りを考えるときは小数点以下の0.8は無視して32で考えます。

よって２桁＋１をした３桁左、元の一の位から３桁左が答えの一の位です。

あくまでも３桁左というのは元の一の位から数えることを間違えないで下さい！

割る数が１未満の小数の場合

では最後に割る数が１未満の小数のケースを紹介します。

割る数が１未満の小数の時は先ほどまでの割る数の桁数＋１左、というわけにはいきません。

小数第１位に０以外の数字があるのか、第２位に０以外の数字があるのかによって、それぞれ元の一の位から１桁左又は０なのかを判断しましょう！

ここはそれぞれを覚えなければいけません。

ただし覚えるといっても、１以上の小数と並べると、１桁ずつずれているのが確認出来ると思います。

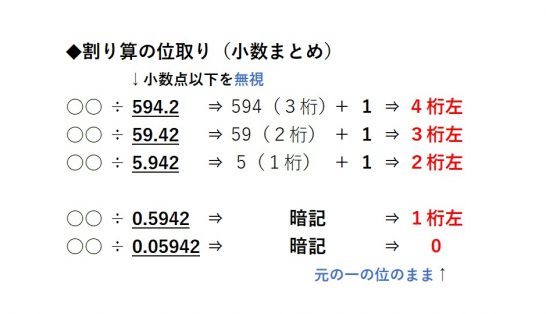
なので、そのことをしっかりと理解できれば、覚えることは簡単です。

位取りはそろばんを進めるうえで疎かにしてはいけない作業になります。

必ず確認してから答えを記入するようにしましょう！

出来れば練習プリントを解いて実際に確認してみることをおすすめします。

⇒⇒割り算の位取り練習用プリントをダウンロード