珠算式暗算の割り算のやり方【÷１桁の計算】
ここでは珠算式暗算の割り算のやり方を解説しています。
内容は割る数が１桁の計算方法です。
もちろん珠算式の暗算なので、そろばんの珠をイメージして計算して下さい！
なお、基本的な解き方はそろばんの割り算のやり方【参考記事】と同じなので、割り算の解き方に不安のある方は参考にして下さい。
ただし、こちらで暗算ならではの解くときのポイントも併せて紹介しているので、必ず確認して下さい。
今回も動画をアップしますので、活用して下さい。
※動画内ではこちらで取り扱っていない問題もあります。
また、このページの内容の練習用のプリントを作成したので、復習にご利用下さい。
７２÷４の計算
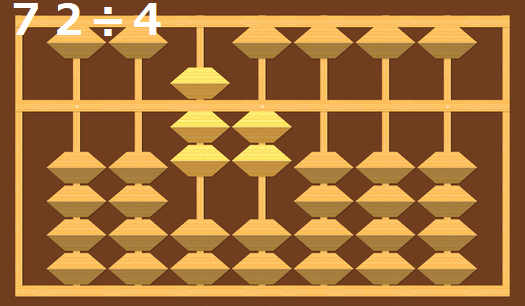
ではさっそく内容に入りますが、まずは７２÷４で確認します。
そろばんが無い状態でも指を動かして、珠を弾くイメージをすると数字を忘れにくくすることが出来ます。
まずは７２を頭の中にイメージします。
もちろん数字の７２ではなく、そろばんの珠の７２です。
感覚的には数字の７２の上に重ねるように、そろばんの珠の７２をイメージします。
もちろん暗算のときはそろばんのように五珠を払ったり、７２を置くイメージはする必要がありません。
そのような動作は必要なく、一瞬でこの７２の状態をイメージして下さい。
計算自体はそろばんのときと同様に割られる数の左側から計算していきます。
なので７÷４から計算します。
７÷４なので、１になります。
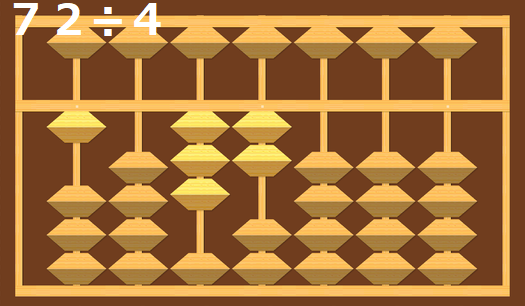
なので、１を入れて、１×４の４を引きます。
この、７から４を引くときの１を入れて、５を取る動作を指を動かしながらイメージしましょう。
残った数は３です。
一の位に２があるので、次は３２÷４を計算します。
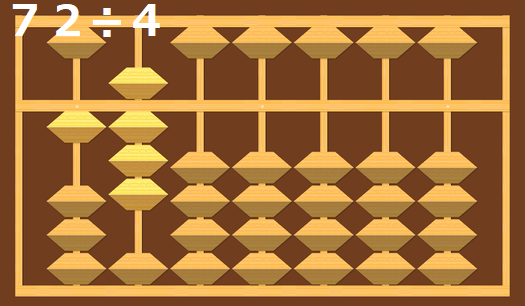
３２÷４は８なので、８を入れて３２を引きます。
これで割られる数は０になったので、答えは１８になります。
暗算で解くときのポイント
割り算を暗算で解くときは一つの引き算が終わった時点で、解答欄に答えとなる数を順に書いていって構いません。
先ほど７２÷４という問題では、７÷４の１を入れて、４を引いたら答えの１を書きます。
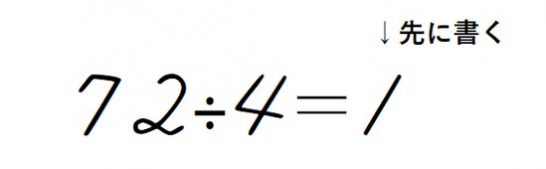そのあとに３２÷４の計算が終わったら８を書きます。
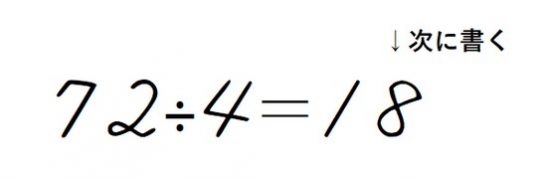
このようにどんどん順に答えを記入していきます。
もちろん簡単な問題であれば、１８を忘れずに計算を終えることが出来ると思います。
ただし、桁が増えるにつれて前に計算した答えを覚えるのが大変になってくると思います。
もちろん理想は覚えておいて、最後にいっぺんに書く方法ですが、まずは解けるようになることを優先して、１つずつ書いて解いてみて下さい。
解説動画内ではこのような解き方で表示しているので、確認してみて下さい。
また、そろばんの時のように、どこの桁に答えを入れるのかを意識する必要もありません。
３２２÷７の計算
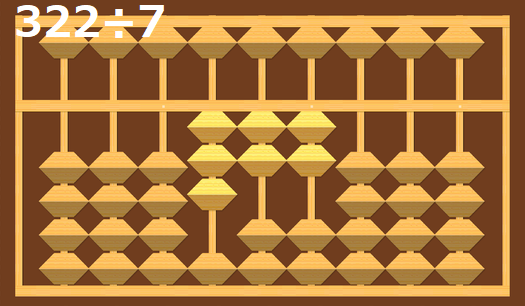
もう１問３２２÷７を使って確認します。
３２÷７なので、４。
４×７の２８を引く。
残った数が４２になるので、４２÷７で６になります。
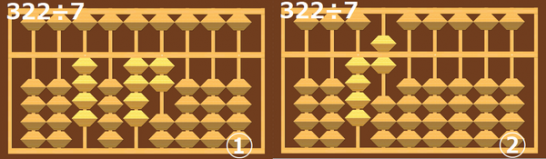
これで４６と答えを求めることが出来ました。
4,620÷5の計算
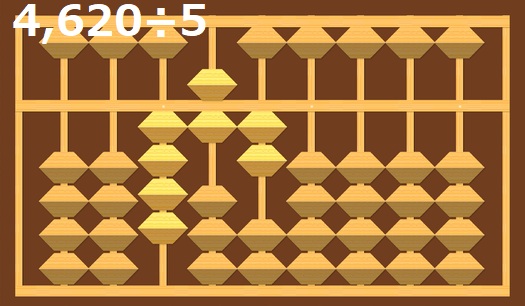
割られるの数の桁数が増えるにつれて、覚え続けるのが難しいと思います。
でも忘れずに完璧に覚え続ける必要はありません。
下１桁や下２桁ぐらいは忘れても問題ありません。
なぜならば問題を見えば書いてあるからです。
なので計算するときはとにかく左側にある２桁、３桁ぐらいに意識を集中させて下さい。
例えばこの4,620であれば、４６に意識を集中させます。
そして４６÷５の９を入れ、９×５の４５を引きます。
そしたら問題を見て２があることを確認すれば、次は１２÷５を考えることがわかります。
１２÷５なので、２を入れて、２×５の１０を引きます。
今度は２が残りましたが、問題を見ると一の位に０があります。
なので、最後に２０÷５を計算し、４を入れ、２０を取って計算は終わりです。
このようにして答えを求めると比較的に楽に解くことができる感覚がわかると思います。
計算の途中経過は以下で確認して下さい。
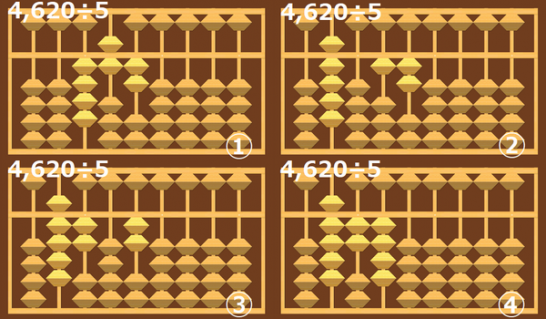
答えは９２４になります。
5,733÷9の計算
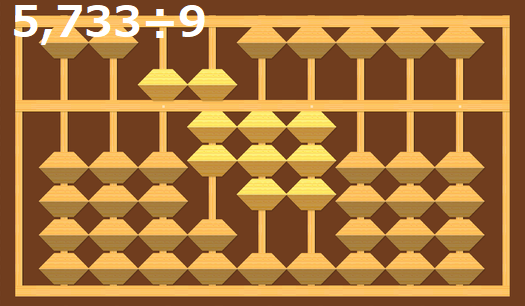
問題の難易度を左右するのは計算パターンの違いになります。
5,733÷9を計算して一つ上の4,620÷5と比べて見て下さい。
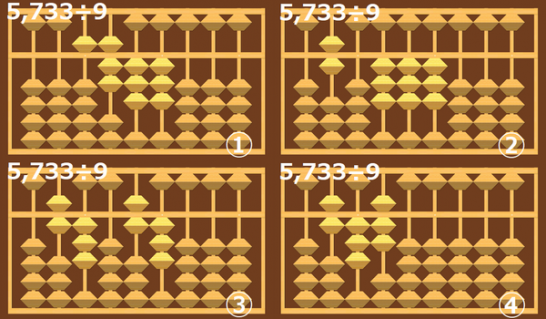
いかがだったでしょうか？
途中の３３から２７を引くような計算パターンが出ると、暗算が苦手な人は難しく感じると思います。
１つ前の５で割った計算よりも難しく感じたのではないでしょうか。
以上が割る数が１桁の割り算を珠算式の暗算で解く方法になります。
今回の内容の練習プリントを作成しましたので、必要な方は復習用にご活用下さい！
このページの学習を終えられた方は次は割る数が２桁の計算に進むことをおすすめします。
暗算検定２級レベルの暗算力を身につける事が出来ます！
PC用広告
公開日：
最終更新日：2018/09/14
