2桁×2桁の計算方法【両落とし】-7級の掛け算講義
7級ではこれまでの8級までと異なり、割る数が2桁となる2桁×2桁の掛け算を学習します。
この講義も本講義のために作成したオリジナルのテキストに沿って、解説を進めるので、先に印刷して手元に用意することをおすすめします。
今回の学習内容に準ずる練習問題も用意しています。
今回も動画解説を中心に、動画下のイラストは補足解説という位置づけで学習を進めていきましょう!
質問等がありましたら、動画内のコメント欄にいただければ返信いたします。
計算前の確認事項
計算の順序
具体的な計算に入る前に、2桁×2桁の掛け算の両落としにおける計算の順番を確認します。
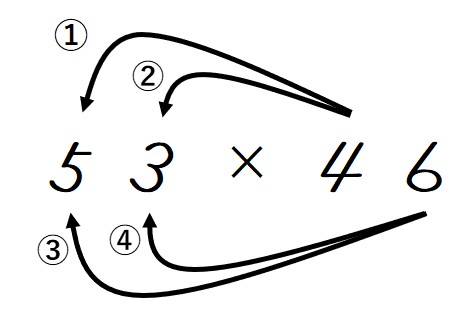
①4×5 ②4×3 ③6×5 ④6×3
の順に計算をします。
10級9級の2桁×1桁を一つの式の中で2回行うイメージを持って下さい。
(1)53×46

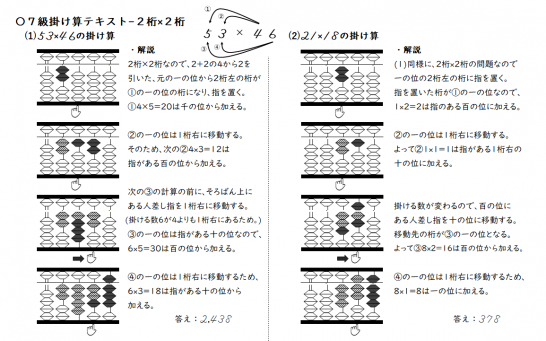
計算の始めに①の計算の一の位を特定します。
特定するルールはこれまでと同じです。
今回は2桁×2桁の計算なので、元の一の位から2桁左の桁(百の位)が、①の計算の一の位になります。
そこに左手の人差し指を置いて計算を始めます。
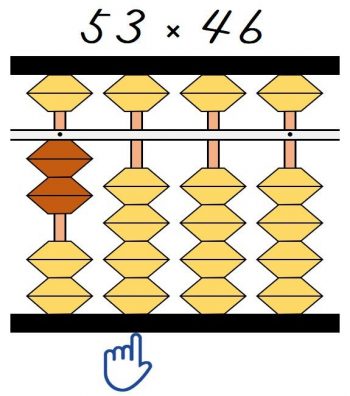
①4×5=20は、指がある桁がその九九の一の位なので、指がある一つ左の桁である、千の位から置きます。
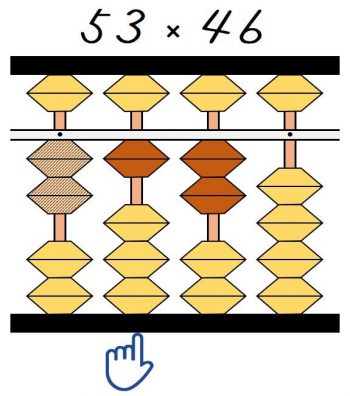
次の②4×3=12の一の位は1桁右の桁に移動します。
なので、12は指がある百の位から加えます。
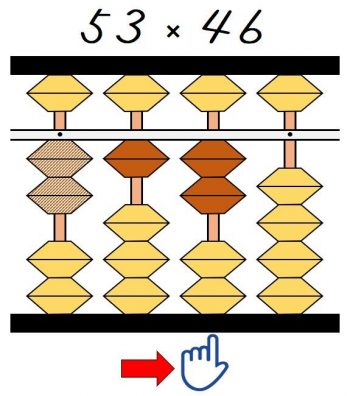
次は掛ける数がこれまでの4から6へと変わります。
掛ける数が変わるとき、これまで百の位に置いていた左手の人差し指を、1桁右の十の位に移動します。
理由としては掛ける数46の6が4よりも1桁右にあるのを反映するためです。
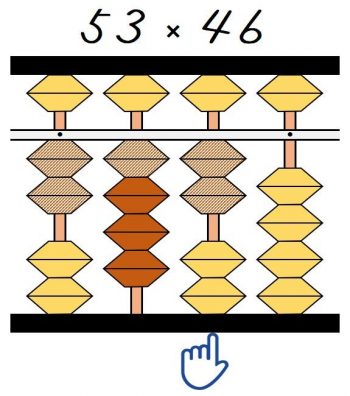
そして次の③の一の位が、指を移動した桁(十の位)になります。
なので③6×5=30は百の位から加えます。
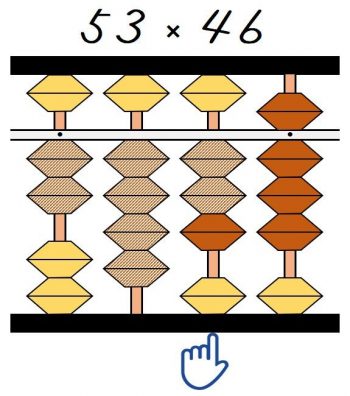
次の④6×3=18の一の位は1桁右に移動するのは②のときと同じです。
なので18は指がある十の位から加えます。
これで計算は終わりになります。
基本的には2桁×1桁の計算を2回行うことになります。
ただし、掛ける数が変わる時に、指を1桁右の桁に移動することになります。
(2)21×18
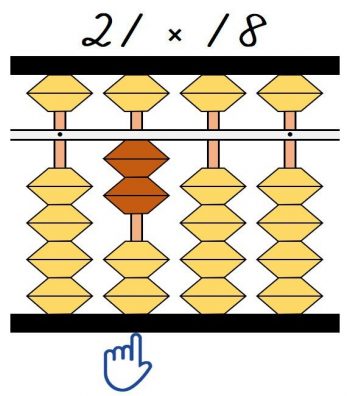
2桁×2桁の問題なので、(1)同様に一の位から2桁左に指を置きます。
指を置いた桁が①の一の位なので、①1×2=2は指がある、百の位に置きます。
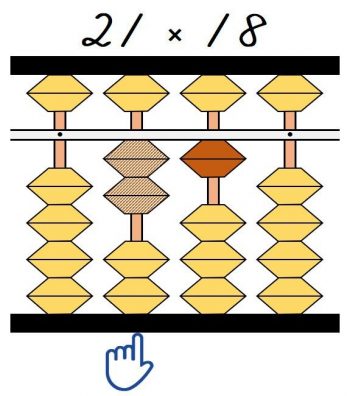
次の②の九九の一の位は1桁右の桁に移動するので、②1×1=1は十の位に加えます。
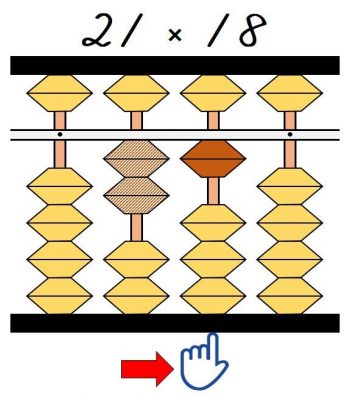
掛ける数が8に変わるので、そろばんに置いてある左手の人差し指を1桁右の十の位に移動します。
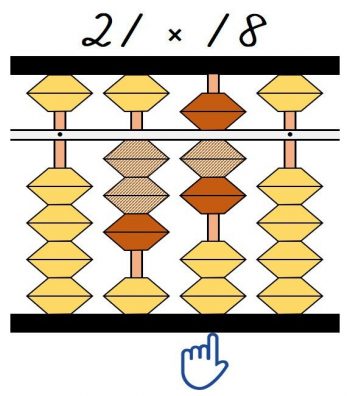
次の③の九九の一の位は新たに指を移動した桁になります。
なので、③8×2=16は百の位から加えます。
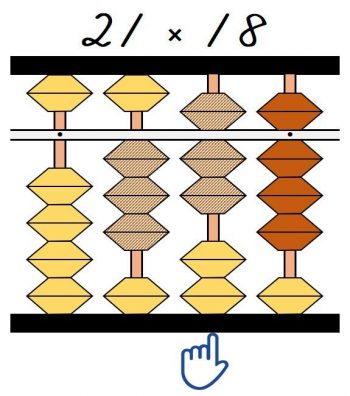
最後の④8×1=8の一の位は1桁右になるので、一の位に8を加えます。
(3)70×35
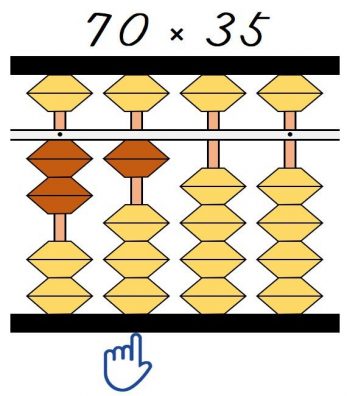
これまで同様に一の位から2桁左に指を置きます。
①3×7=21は千の位から入れます。
次の3×0は0なので、何もする必要がありません。
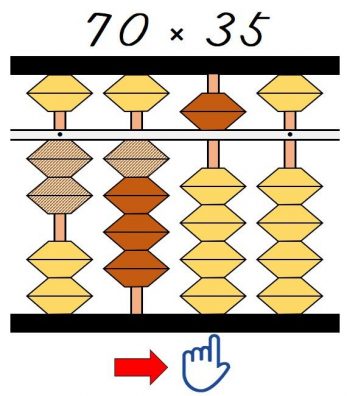
掛ける数が5に変わるので指を1桁右の桁に移動します。
そこが次の計算の一の位なので、②5×7=35は百の位から加えます。
最後の5×0も不要なので、これで計算は終わりです。
掛ける数の時に指を移動することを忘れないで下さい。
今回の解説は以上になります。
ポイントは、掛ける数が変わる時に左手の人差し指を1桁右の桁に移動することです。
始めは一つ一つを考えながら解くことになりますが、慣れるとリズムよく解くことができると思います。
テキストに付属の練習問題を使ってぜひ練習してみて下さい!
PC用広告
公開日:






