そろばんの割り算における小数点の決め方と計算方法

このページではそろばんの割り算における小数点の位置の決め方と、小数の問題の計算方法を解説しています。

後半では検定試験で四捨五入が必要になる問題の解き方を解説します。

そろばんで割り算の小数の問題を解くには、計算方法が新しく何か変わるものではありません。

大切なのは小数点の位置の決め方(位取り)を覚えることです。

特に位取りというものがよくわからないという方は、この先を読み進める前に、割り算の位取り解説【参考記事】を読んで下さい！

小数の割り算の問題のみを集めた練習用プリントを作成しましたので、ご利用下さい！

⇒⇒小数の割り算練習用プリントをダウンロード

ではここから解説に入りますが、以下の解説では計算の途中過程は省略しています。

途中の計算過程も含まれている動画解説も活用することをおすすめします。

小数の割り算の計算方法

具体的な計算方法の前に、まずは小数点の位置の決め方を復習します。

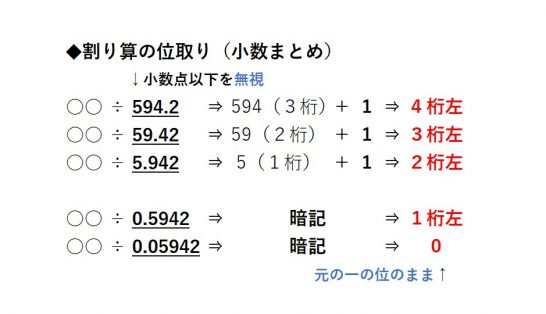
割る数が１以上の小数の場合は、小数点以下を無視します。

そして整数の部分の桁数に＋１をした桁数、元の一の位より左にずれた桁が答えの一の位（小数点の位置）になります。

割る数が１未満の小数の場合は、それぞれのパターンを覚えなければいけませんでした。

11,973÷3.07の計算

問題の数字をそろばんに置いた後に、計算する前に位取りを行います。

今回は割る数が3.07なので、元の一の位(３の桁)から２桁左が答えの一の位になります。

ここに計算をする前に左手の人差し指を置きます。

そしてこの状態で計算を行います。

先に位取りを行うのが掛け算との違いであり、小数の割り算のポイントになります。

先に置く理由は後半で説明する四捨五入に関係します。

なお、計算自体は307と同じように計算します。

計算した後は上のような状態になります。

もちろん計算の最中も左手の人差し指は同じ位置に置いたままです。

つまり答えは3,900になります。

14,976÷0.32の計算

続いて14,976÷0.32で確認します。

先ほど同様にまずは先に位取りを行い、答えの一の位となる桁に予め左手の人差し指を置きます。

今回は割る数が0.32なので、元の一の位から１桁左になります。

１未満の小数のときも、計算する際は３２と同じように計算します。

計算後はこのようになります。

よって答えは46,800になります。

四捨五入が必要な小数の計算

続いて75÷0.81の計算を使って、検定試験で四捨五入が必要となる問題の解き方を解説します。

珠算検定試験では、掛け算とともに割り算も割り切れない場合は、前半は小数第３位までの数字を求めます。

そのために小数第４位の数を四捨五入しなければいけません。

また、後半の問題は答えを整数にしなければいけないため、小数第１位まで求め、四捨五入をします。

小数第１位を四捨五入

はじめに後半の整数の答えを求めるケースを解説します。

まずはこれまで同じように、先に位取りを行い、答えの一の位となる桁に左手の人差し指を置きます。

割る数が0.81なので、元の一の位の１桁左になります。

そのまま計算するのですが、この問題は答えを割り切る事が出来ません。

つまり、延々と計算が続きます。

なので、今回は答えの小数第１位の桁まで求めればいいのです。

つまり、そろばんに置いてある指の１桁右の桁までになります。

その結果が以下のようになります。

小数第１位まで答えを置くことが出来たら、四捨五入をします。

今回は５なので、切り上げた９３を答えとして解答用紙に記入します。

なお、そろばんの上に残っている元の数は完全無視で構いません。

慣れないうちは小数第１位の５を取って繰り上げて９３にしてから答えを書きましょう。

慣れたら92.5の状態で９３を書くようにすると無駄な時間もなくいいでしょう！

小数第４位を四捨五入

では次に答えを小数第３位までにするために、小数第４位を四捨五入するケースになります。

先ほど小数第１位まで求めたものになります。

あと３桁答えを求めることで小数第４位まで埋まります。

そのまま計算を続けましょう。

小数第４位まで求めるとこのようになります。

指が置いてある桁の３桁右まで答えを置きます。

そして四捨五入です。

よって答えは92.593になります。

以上が小数の割り算の計算方法になりますが、掛け算との違いはどのタイミングで位取りを行うかになります。

割り算の場合は割り切れないことがあるので、どこの桁まで計算したらいいのかわかりやすいように位取りを行うことになります。

もちろん絶対先にやらなければいけないルールはないのですが、初めはこの方法の方が間違いが少なくていいと思います。

指を先に置かないと小数第１位まで計算すればいいのに、第２位、３位までと無駄に求めてしまうことがあるので注意して下さい。

実際に問題を解いて自分に合ったやり方を探してみて下さい！

⇒⇒小数の割り算練習用プリントをダウンロード