3桁÷1桁/4桁÷1桁の計算方法-7級割り算講義
一つ前の8級から始まった割り算の学習ですが、今回の7級はその延長の位置づけです。
前回同様に割る数が1桁になり、8級では商が2桁だったのに対し、7級では商が3桁になります。
基本的な考えは8級と同じですが、7級ならではの論点としては(3)の問題になります。
もちろんこの講義も解説テキスト&練習プリントを作成しましたので、それに沿って解説を進めていきます。
印刷して手元に用意することをおすすめいたします。
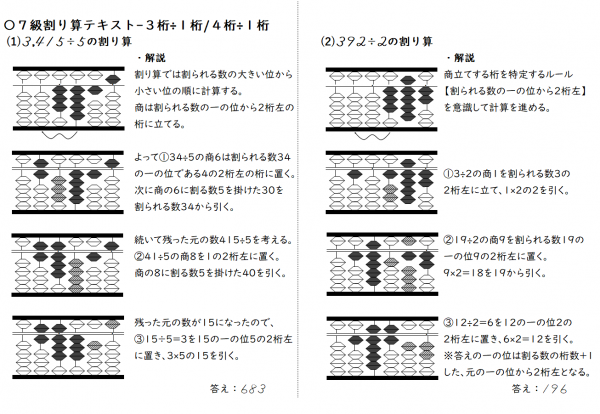
今回も動画解説を中心に、動画下のイラストは補足解説という位置づけで学習を進めていきましょう!
質問等がありましたら、動画内のコメント欄にいただければ返信いたします。
(1)3415÷5
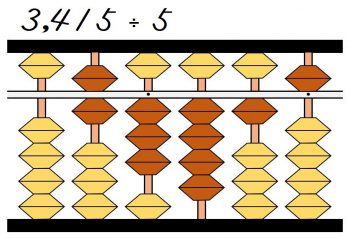
割り算は式の左側の割られる数の大きい位から順に計算していきます。
なので始めに34÷5を考えます。
商は6になります。(余り4は不要)
この6を4の2桁左である一万の位に立てます。
※この割り算の商を立てる桁を決めるルールについては8級の講義【参照】を参考にして下さい。
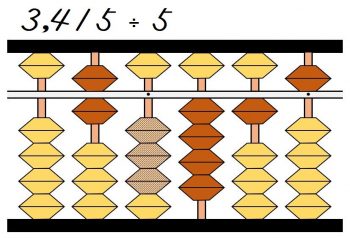
商である6を立てたあとは、商の6に割る数5を掛けた6×5=30を、割られる数34から引きます。
これで残った割られる数は415になりました。
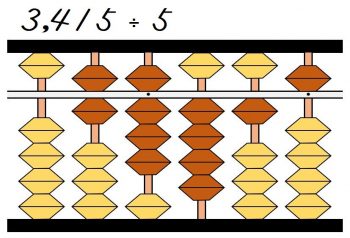
次は残った415の中で、41÷5を考えます。
41÷5なので、商は8になります。
よって千の位に8を置きます。
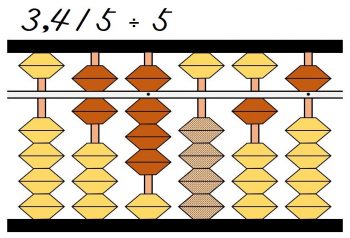
商を立てたら先ほどと同じように、商の8に割る数5を掛けた8×5=40を、41から引きます。
すると残った元の数は15になりました。
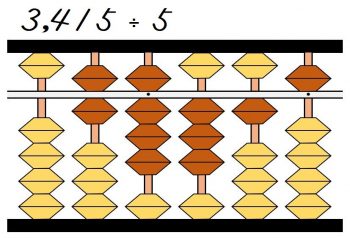
最後にこれまでの手順と同様に、残った15÷5を考えます。
商は3になるので百の位に3を立てます。
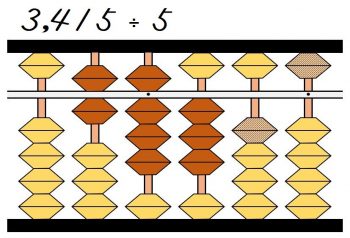
そして3に割る数5を掛けた3×5=15を引きます。
これでそろばんの上に残っていた3415は0になったので、計算は終わりです。
割り算では計算後に必ず答えの一の位を把握(位取り)しなくてはいけません。
この問題の割る数は1桁なので、+1をした元の一の位から2桁左が答えの一の位になります。
よって答えは683になります。
※位取りのルールも8級の講義【参照】にて詳しく解説しています。
(2)392÷2
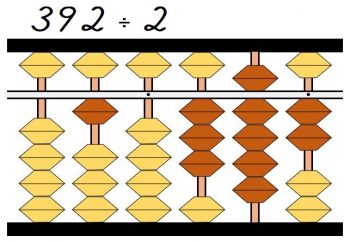
(1)同様に割られる数の大きい位から計算を考えます。
今回は3÷2になります。
3÷2なので、商の1を3(一の位)の2桁左の一万の位に立てます。
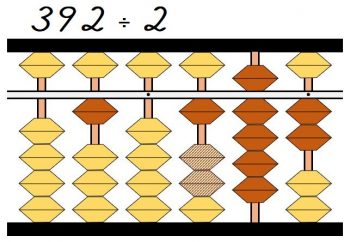
商を立てたら、商に割る数を掛けた2×1=2を引きます。
残った数は192になります。
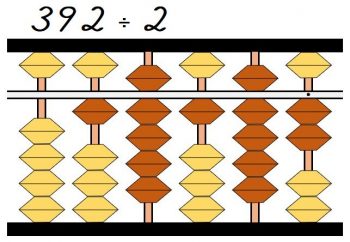
次は1÷2は不可なので、隣の桁を含めた19÷2を考えます。
商は9になるので、千の位に9を置きます。
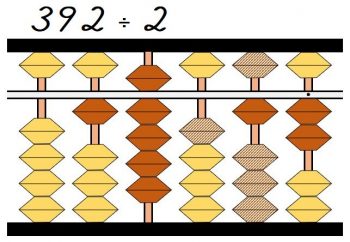
商を立てたら先ほど同様に割る数を掛けた9×2=18を引きます。
そろばん上に残った元の割られる数は12になりました。
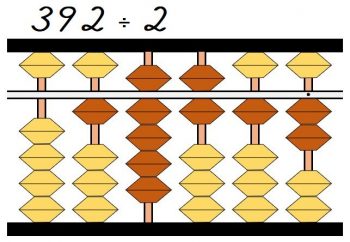
最後に残った12÷2を考えます。
商の6を百の位に置きます。
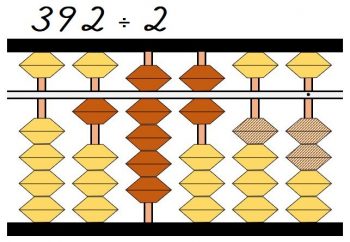
商の6に割る数2を掛けた6×2=12を引き、元の割られる数は0になりました。
最後に答えの一の位を忘れずに確認するようにして下さい。
答えは196になりました。
(3)1208÷4
最後に7級ならではの論点が含まれる問題を解説します。
この問題は答えを立てる桁を正しく把握するに尽きます。
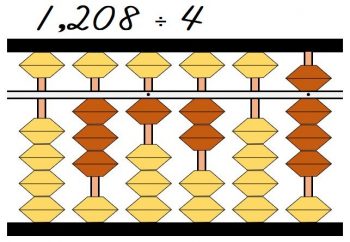
まずは12÷4なので、商の3を一万の位に立てます。
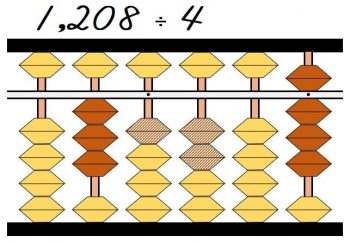
これまでのように、商の3に割る数4を掛けた3×4=12を引きます。
そろばん上に残った元の割られる数は8になりました。
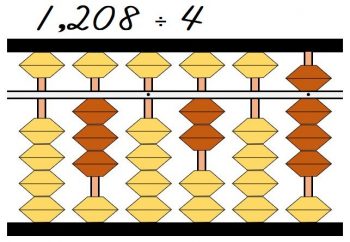
次は残った8÷4なので、商の2を8の2桁左の百の位に立てます。
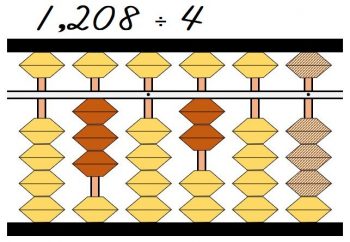
そして2×4=8を引きます。
答えの一の位は元の一の位から2桁左になるので、答えは302になります。
計算としては簡単ですが、繰り返しになりますが商を立てる桁を正しく把握して下さい。
答えを320や32にしないように注意しましょう。
商を立てる桁を考えるのはあくまでも割られる数をベースとします。
一つ前に自分が立てた商の隣の桁に置きたくなるのもわかりますが、過ぎ去った計算の商は無視して下さい。
今回の解説は以上になります。
練習問題をうまく活用し、模擬検定にもチャレンジしてみましょう!
PC用広告
公開日:






