○○÷2桁の問題をそろばんで解く方法
このページではそろばんの割り算のやり方を解説しています。
今回の内容は「○○÷2桁」の計算になります。
割り算の応用へと入る第1歩目になります。
検定試験では6級の内容になります。
※ここでは還元の問題(戻し算)は取り扱ってません。
還元の問題(戻し算)のみを扱った解説ページをご覧下さい。
途中過程がわかる動画を参考に学習を進めることをおすすめします!
動画内では以下の解説で扱っていない問題も含んでいます。
今回の割る数が2桁の問題を集めた練習用プリントもご活用下さい!
割る数が2桁の計算方法
204÷68の計算
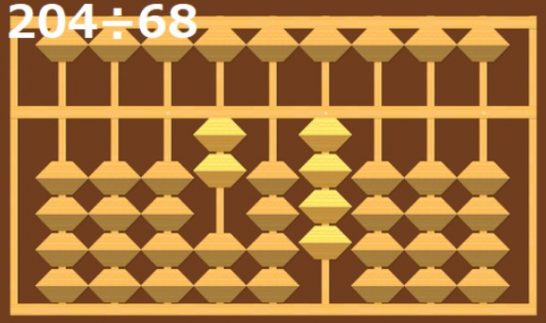
はじめに204÷68を解説します。
式の右側の割る数が68と2桁になりますが、計算する順番は割られる数(式の左)と割る数のそれぞれの左側(大きい桁)の数同士で考えます。
なので、2÷6になります。
しかし、2÷6は1以上の答えがないため、次の桁まで含めた20÷6で考えます。
20÷6なので、3をそろばんに入れます。
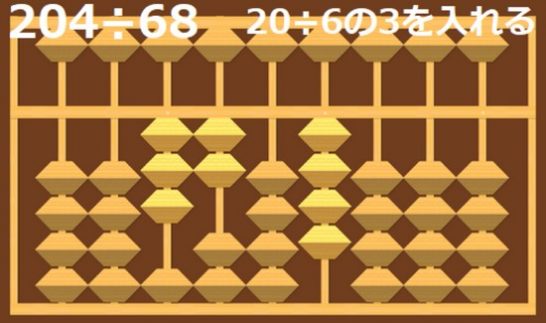
余りのある割り算の答えを出す方法や、珠の置く場所の決め方は今回は省略します。
詳しくは2桁÷1桁の解説ページ【参考記事】をご覧下さい。
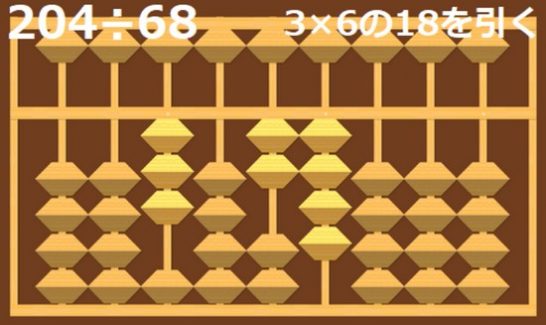
3を入れたら、置いた3×6の18を20から引きます。
ここまでは今までの計算とほとんど同じです。
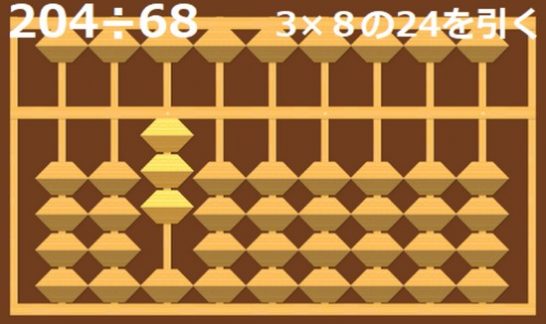
次に、置いた3に今度は68の8を掛けた、3×8=24を引きます。
このとき、引く数は一の位が1桁右にずれます。
68の8は6(十の位)に対して、1桁右(一の位)にあるからです。
その分引く桁も1桁右に反映してあげます。
これで元の数は0になりました。
よって計算は終わりになります。
そして答えは3になりました。
割る数が2桁の割り算ポイント
割る数が2桁の計算では、最初に珠を置いたら、そのあとに2回引き算を行います。
その際に、一の位が1桁右にずれることを忘れないで下さい。
「1回置いたら2回引く」と覚えて下さい!
また、2回目を引くときに、新しい答えを置かないように注意して下さい。
一度答えを入れたら、2回引き算を行うリズムを覚えましょう!
144÷16の計算
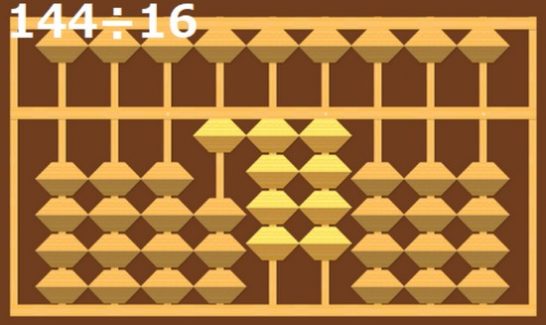
続いて144÷16の計算を考えます。
少し難しいのですが、とても大事な新しい知識が含まれるので、しっかりと理解して下さい!
まずはこれまでと同様に計算してみましょう!
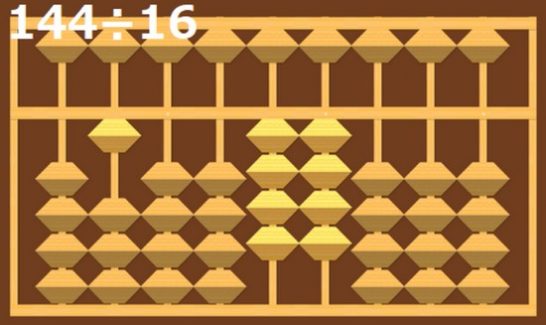
はじめに式の左側同士を計算するので、1÷1で1になります。
よって、1を入れて、置いた1に÷数1を掛けた1×1の1を引きます。
次は入れた1に割る数16の6を掛けた6を引きますよね?
しかし、今回は先ほど引いた144の1があった1桁右の桁に6がありません。
なので引くことが出来ません。
ではこのような場合はどうするのか?

今回の問題のように、式の左側の数同士が同じ数の場合、2÷2や5÷5など、そのときはその隣の桁まで含めて比べます。
すると14÷16になります。
そして右側の割る数の方が大きいときは、14÷1と考えて4の2桁左に9を置きます。
なんで9なの?というよりは、9を置くルールとして覚えて下さい。

あとは同じように、置いた9×1の9を14から引きます。
続いて9×6の54を引きます。
これで元の数は0になります。
よってこの問題の答えは9になります。
9を置く問題のポイント
式の左側同士の数が同じならば、その次の桁の数も含めて2つの数を比べる。
右側の割る数が大きいときは9を置く。
216÷27、342÷38などが、同じ種類の問題なので、試してみて下さい!
こういった問題をいろいろ問題が混同した中で気づけるかが大事なポイントになります。
なお、左側の割られる数の方が大きいときは、1を置いて計算を進めて下さい。
初めは気付くのが難しいと思いますが、こういう内容があることは知っておいて下さい!
672÷21の計算
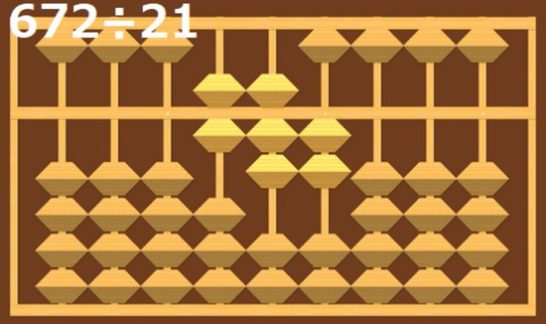
では続いて672÷21の問題を考えます。
答えが2桁になる応用とも言える内容になります。
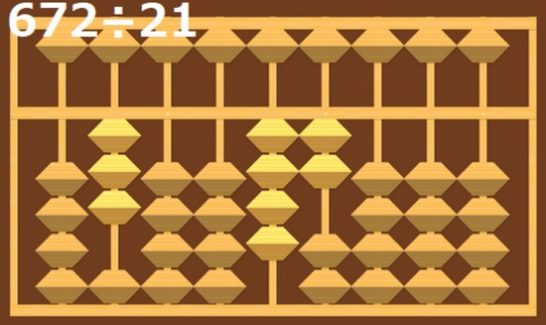
まずは6÷2の3をそろばんに入れましょう。
そして置いた3×2の6を引きます。
続いて置いた3に21の1を掛けた3を1桁右の桁から引きます。
ここまでは今までと同じです。
今まではこれで元の数は0になっていたので、計算が終わっていたのですが、この問題ではまだそろばんの上に42が残っています。
よってそろばんに残った42÷21を計算します。
また新しい答えを置くので、式の左側同士で割り算を行います。
4÷2なので、2をそろばんに入れます。
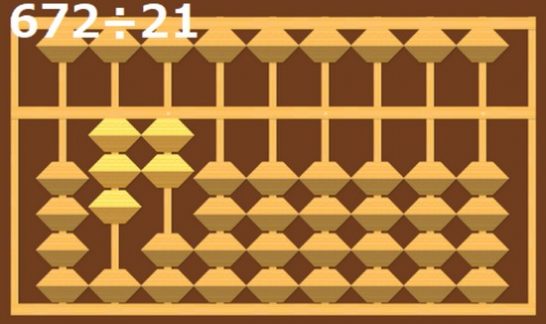
そうしたら4の2桁左に2を置いて、あとは同じように置いた2に21の2を掛けた2×2=4を引きます。
そして次に置いた2に21の1を掛けた2×1=2を引きます。
これで元の数は0になりました。
そしてこの問題の答えは32になりました。
この問題では上で説明した答えの珠を置いたら2回引くというのを、2回繰り返しました。
割る数が2桁の割り算では、この1回置いたら2回引くというのを、元の数が0になるまで繰り返します。
8,815÷43の計算
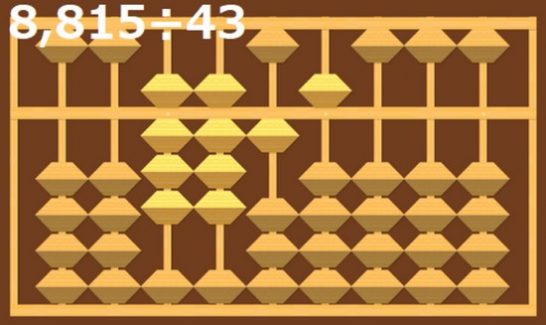
最後に8,815÷43を考えます。
答えを入れる桁に注意して計算を進めましょう!
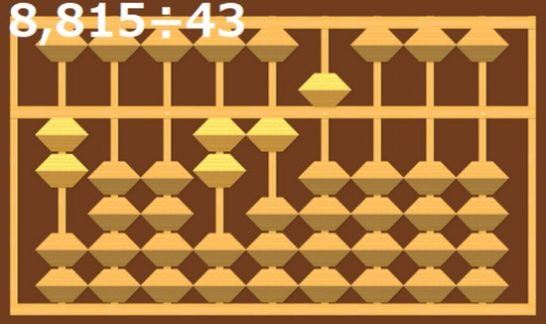
8÷4から考えるので、2になります。
8の2桁左に2を入れて、2×4の8を引きます。
次に2×3の6を1桁右の桁から引きます。
するとそろばんの上には215が残りました。
なので、215÷43を計算します。
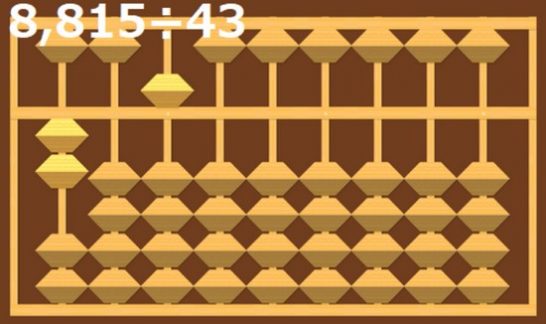
21÷4を考えるので、5を入れることになります。
21の1が一の位なので、ここの2桁左に5を入れます。
そして置いた5×4の20を引き、最後に5×3の15を引いて、計算は終わりです。
答えは205になりました。
この問題の細かい計算過程は以下で確認して下さい。

繰り返しますが、答えを入れる桁は割られる数を基準に考えます。
間違えないようにしましょう!
以上で割る数が2桁の計算の解説を終わります。
本格的な割り算の計算に入りましたので、しっかりとそろばんを使って練習問題を解くことが大切になります。
2桁の割り算理解出来た人は割る数が3桁の割り算に進むことをおすすめします。
PC用広告
公開日:
最終更新日:2021/12/25






