暗算が出来る人の頭の中を覗き見！ ～日常生活での計算方法～

日常生活を送っていて、本当に計算が必要になる場面は正直なかなかないと思います。

しかしそろばん経験者、特に暗算が出来る人であれば、必要もないのに頭の中で計算をしてしまっているのではないでしょうか…？(私だけ…!?)

そろばん経験者あるあるであって欲しい…。

計算と目にすると、無駄に頭を使って…なんて思われるかもしれませんが、暗算ができる人にとっては対したことではないんです。

というより、ある種職業病？というか習慣的にもはや勝手に計算をしていたりするんですよね(笑)

代表的なのが買い物のおつりや、消費税の税込み価格の計算の２つです！

今回はこの２つの例を使って、暗算が出来る人の頭の中で考える計算のプロセスを紹介します。

計算が速い人ってこうやって考えてるんだぁと感じていただければと思います。

ちなみに今回この記事を書こうと思ったきっかけが、よく行くパン屋さんにどうやって考えているのか聞かれたからです。

街のパン屋さんやお肉屋さんってレジがあっても手打ちだったりしますよね？

よく行くお店だと私が計算できることを知っているので、他に人がいないときに合計金額や税込み価格をクイズにされるんですよね…。

そこで一瞬で頭の中に数字が浮かぶのか聞かれたのですが、そうではないので今回紹介することにしたのです。

買い物のおつり

まずは買い物のおつりを計算する際に、頭の中で考えている方法を紹介します。

500円、1000円など切りのいい金額を出したとき

例えば632円の物を買うときに、代金を出す際に1035円や1050円、1005円などというように、千円札＋小銭を出すことがあると思います。

まずは財布に小銭がなかったときに1000円、5000円といった切りのいい金額を出したときのおつりを計算する際に頭の中で考えていることを紹介します。

えっ!?いくら出しても引き算すればいいんじゃないの？と思われた方もいるかもしれません。

確かにそうです。

もちろん真正面から1000-632=368と、おつりの368円を暗算で出すことも出来ます。

しかし実際には私の場合は異なる方法をします。

それは632にあといくらで1000になるかを考えるのです。

頭の中を具現化すると以下のような状態です。

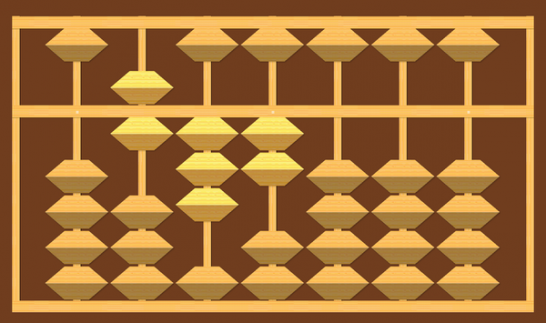
こんな感じで632がスタートです。

1000ではないんです。

ここから1000にするために必要な数字を考えます。

考えるといっても一瞬(いや、１秒か？)ですが…。

このとき一の位以外は合わせて９になる数を探します。

そして、一の位は合わせて10になる数を探します。

なので、百の位６の相手は３、十の位の相手は６、一の位２の相手は８となり、おつりの金額である368円を出しています。

これはそろばんの見取り算の中にある、補数計算(マイナスの計算)の答えを書くときの考え方に基づいています。

そろばんを習うとこういった考え方で計算をすることも出来るのです。

繰り下がりで頭を使う必要がないので、引き算をするよりも簡単なのです。

1738円の物を買うときに5000円を出した場合であれば、千の位は４になるように考えます。

百の位と十の位は９、一の位は10になるように相手の数を考えると、3262円と求めることが出来ます。

切りのいい金額ではないとき

今度は1000円や5000円といった切りのいい金額ではなく、632円の物を買うときに1035円、1050円、1005円といった金額を出した際のおつりの計算をする際の頭の中での計算方法です。

このような場合は頭の中で引き算をします。

桁の大きい方からそろばんを行うように暗算します。

それでも数字を分けて少し簡単に計算することも出来ます。

1035円であれば、10-6と35-32に分けて、それぞれの答え4と(03)を合わせて403円を求めることが出来ます。

1050円であれば、10-6=4、50-32=18を合わせて418円。

1005円のときは100-63=37、5-2=3で分けて373円と出すことが出来ます。

計算の工夫を頭の中で半ば無意識的に行っているのです。

消費税の計算

続いて消費税(税込価格)を計算するときの頭の中のプロセスをご紹介します。

消費税は５％のころは本当に計算が楽でした。

８％になり少し面倒になりましたが、計算過程は全く同じです。

例えば1680円の商品の税込み価格を求める場合。

８％なので、0.08かけると消費税分を出すことができ、1.08をかけることで税込み価格を求めること出来ます。

だたし、私が求めるときはややこしくなるので、0.08や1.08といった小数を意識することはありません。

８という数字のみ意識します。

そして1680の桁が大きい左側の数字に８をかけた数を求めて、1680に足していきます。

①1000に８％をかけた80をだし、1680に足す。このとき1760になる。
②600に８％をかけた48をだし、1760に足す。1808になる。
③80に８％をかけた6.4をだし、1808に足す。1814.4になる。

最後は0.4の部分を四捨五入して1814円を求めています。

今の上で説明したプロセスを頭の中で経て、税込み価格を求めているのです。

決して頭の中に数字が思い浮かぶというようなことではなく、しっかり計算をしているのです。

実際にはこの作業は１秒もかからずに求めることが出来ます。

これはやはりそろばんを習うことで得られた暗算力のおかげです。

もちろん日常生活で暗算で計算が出来なければいけないことなんてありません。

それでも暗算が出来るといろいろと楽しいものです。

中学、高校といった勉強でも計算が速いことで様々なメリットがありました。

良かったら少しでもそろばんに触れてみて下さい！